Ion-molecule Collision Reactions in Gas-Phase

In mass spectrometry, ion-molecule reactions refer to the chemical reactions that take place between charged ions and neutral molecules within the gas phase of the instrument. These reactions can occur either before or after the ions are introduced into the mass spectrometer. In ion-molecule reactions, the analyte ions collide with a neutral gas molecule, resulting in the transfer of energy to the analyte ion and fragmentation of the ion into smaller product ions. The product ions can then be analyzed to provide structural information about the original analyte molecule. Soft ionization mass spectrometry, based on the chemical ionization (CI), refers to ionization techniques that generate molecular ions with little or no fragmentation, producing a mass spectrum that is dominated by the molecular ion peak. Soft ionization techniques are particularly useful for the analysis of complex molecules, such as biomolecules and natural products, which are often prone to fragmentation under high-energy ionization conditions. Soft ionization techniques, such as electrospray ionization (ESI) are valuable in the analysis of complex mixtures, as they can provide detailed information on the composition and structure of the analytes without significant fragmentation. These techniques have a wide range of applications in fields such as proteomics, metabolomics, and natural products research.

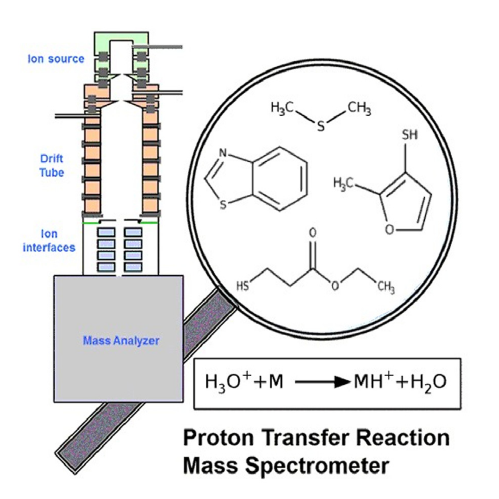
Image credit: M. Bhatia et al. JASMS, 2022.

 Ion-molecule reactions are indeed generally fast and exothermic, and they can occur at every collision between an ion and a molecule. During these reactions, energy is transferred between the ion and the molecule, leading to the formation of product ions. The rate of ion-molecule reactions depends on several factors, including the collision energy, the concentration of the reactants, and the properties of the reactant molecules and ions. In general, higher collision energies and reactant concentrations can increase the rate of ion-molecule reactions. An ion-molecule reaction with zero activation energy is a reaction in which the reaction barrier between the reactants and products is so low that the reaction occurs without any significant activation energy. In other words, the reaction occurs as soon as the reactant ions and molecules come into contact with each other. In such a reaction, the kinetic energy of the ions and molecules is sufficient to overcome the potential energy barrier between the reactants and products, leading to the formation of product ions without the need for additional energy input. This can occur in some types of ionization techniques, such as CI, where the ion-molecule reaction occurs at atmospheric pressure without additional energy input.

  Various theoretical approaches based on capture collision theory have been developed to compute the rate coefficients of ion-molecule reactions in gas-phase. These theoretical approaches require electric dipole moment and polarizability of the neutral molecule as input parameters for the rate coefficient calculation. Further, electric dipole moment and polarizability of the molecules can be obtained from quantum chemical calculations for cases where experimental values are not available. The rate coefficients of reactions (which are fast, exothermic) are generally equal to the collision-rate coefficients, typically of the order of $10^{-9}$cm$^3$ s$^{-1}$.
Often, ion-molecule reactions are among the fastest chemical reactions known, as the electrostatic interaction between the ion charge and the polar molecule draws these reactants together at a long range attractive force.
In any ion-molecule interaction, an approaching ion distorts the charge distribution in the molecule and a region of opposing charge will be drawn towards the approaching ion, thus creating a dipole moment in the neutral molecule.
Commonly used theoretical approaches to evaluate ion-molecule reactions in CI-MS instruments are discussed below:

Pure Polarization Theory (Langevin Model)

The Langevin theory provides a good description of ion-molecule collision reactions for a non-polar molecule. Where, the ion is treated as a point charge while the non-polar molecule is treated as a point particle. This ion-induced dipole interaction is attractive. Therefore, the more polarizable the neutral molecule, the stronger will be the attraction for a given ion-molecule separation. In the ion-nonpolar molecule, long-range ion-induced-dipole interactions dominate. The long-range potential in the ion-induced-dipole is given by

$$V(r) = -\frac{1}{4\pi \epsilon_0} \frac{\alpha {q^2}}{2r^4},,$$

where $q=z,q_{e}$ is the charge of the ion ($q_{e}$ is the elementary charge in Coulomb);
$\alpha$ is the polarizability of the neutral species, $r$ is the distance between the centers of mass of the ion and neutral molecule.
The theoretical evaluations of the rate coefficient by Langevin cite{langevin} is as follows,

$$ {\rm k}_{\rm Langevin}=\sqrt{\frac{\pi \alpha q^{2}}{\mu \epsilon_{0}}}
,,$$

where $q$ is the charge of the ion ($q=z,q_{e}$, where $q_{e}$ is the elementary charge in Coulomb); $alpha$ is the polarizability of the neutral species; and $mu$ is the reduced mass of the reactants. The Langevin theory predicts rate coefficients for collisions between ion and non-polar molecules in the high temperature limit, and computed rates can not be applied to polar molecules.

Average Dipole Orientation Theory (ADO)

Average dipole orientation (ADO) theory as given by Su and Bowers provides a more refined description of ion-molecule collision by considering the interaction between the ion and the permanent electric dipole of the neutral molecule. For polar molecules, a more improved model as compared to Langevin includes ion-dipole forces in addition to the ion-induced-dipole forces. In this case, the interaction potential has the form
$$V(r, \theta) =-\frac{1}{4\pi \epsilon_0} \frac{\alpha {q^2}}{2r^4} -\frac{1}{4\pi \epsilon_0} \frac{q\mu_{\rm D}}{2r^2}cos{\theta}$$

Here $\mu_{\rm D}$ is the dipole moment of the neutral molecule and $\theta$ is the angle the dipole makes with the line of centers of the collision. The long range forces, ion-induced dipole and ion-permanent dipole forces contribute toward increasing rate coefficients.
However, the extent of their contribution largely depends on the electric dipole moment. The capture collision rate coefficient from ADO is obtained by the equation below:

$${\rm k}_{\rm ADO} =
{\rm k}_{\rm Langevin}
+\frac{C\mu_{\rm D}, q}{\epsilon_0}\sqrt{\frac{1}{2\pi \mu \it k_{\rm B} T}}$$

Here $C$ is a locking parameter which depends on the degree that the dipole is aligned with the ionic charge during the collision, and valued $C$ ranges between 0 (no-alignment) to 1 (locked dipole). The $C$ parameter depends on the electric dipole moment $\mu_{\rm D}$ and polarizability $\alpha$ of the neutral molecule. The dependence of $C$ on temperature and $\mu_{\rm D}/\alpha^{1/2}$ can be evaluated from the procedure suggested by Su. Many authors used the ADO method to evaluate reaction rates between H$_{3}$O$^{+}$ and VOC molecules. However, ADO theory was successful in estimating reaction rates at many room temperature collisions conditions, but several comparisons with experiment show underestimation of ADO rates, typically by 10-20%. The reason for this lies in the non-zero dipole moment of the ionic reactant (H$_{3}$O$^{+}$), which is considered as a point charge in ADO theory. It is expected that as compared to H$_3$O$^+$ ions, symmetry makes the dipole moment of NH$_{4}^{+}$ vanish: therefore, the ADO theory applied to NH$_{4}^{+}$ ion tends to agree better with experiments.

The ADO theory provides a fair initial estimation of the rate coefficients where experimental results of ion-molecule rate coefficients are not available.

Classical Trajectory Method

Later, Su and Chesnavich performed trajectory calculations to estimate rate coefficients in order to improve beyond the ADO model. The model assumes ions as a point charge and the polar molecule as a two-dimensional rigid rotor. Based on the above assumptions, Su revised the trajectory method and obtained rate coefficients at a broad range of temperatures through a series of classical trajectory calculations. Rate coefficients obtained were consistent with experimental rates within a 3% accuracy. The following equations describe the trajectory model and the parametrized expression:
$$\rm k_{\rm capture}(\it T,{\rm CT})=\rm k_{\rm Langevin}$$ , $$\it K_{\rm capture}(T_R, {I}^{\star})$$,.
The parameterized quantity $$K_{\rm capture}(T_R, {I}^{\star})$$ is a function of two reduced parameters: the dimensionless reduced temperature $$T_{R}$$ and the moment of inertia $$I^{\star}$$ of the neutral molecule. Here, $$T_{R}=4\pi \epsilon_{0} \frac{2 \alpha k_{B}T}{\mu_{\rm D}^2}$$ and the dimensionless parameter
$$I^{\star}= \frac{\mu_{\rm D}I}{\alpha q \mu}$$
,. $$I$$ is the moment of inertia of the neutral molecule and other symbols are the same as defined earlier. The results from various trajectories obtained by Su and Chesnavich suggested that the value of $$K_{\rm capture}$$ is insensitive to $$I^{\star}$$ when
$$I^{star} < frac{0.7+x^{2}}{2+0.6x},, where x= T_{R}^{-1/2} $$,. For reacting systems we come across the molecular species studied in PTR-MS, the values of $\alpha$, $\mu_{D}$ and $I$ are such that $K_{rm capture}$ lies in the insensitive region following above inequality. Under such circumstances, $K_{\rm capture}$ depends only on $T_{R}$, i.e. on $x$, and its value is parameterized as follows:$$ K_{\rm capture}=\begin{cases} ({x}+0.5090)^2/10.526+{0.9754}, & x \leq 2\ 0.4767,\\ x+0.6200, & 2 < x \leq 3\ 0.5781,\\x+0.3165, & 3 < x \leq 35\ 0.6201,\\x-1.153, & 35 < x \leq 60\ 0.6347,\\x-2.029, & x < 60 ,. \end{cases}$$ Collision-based models are often used for the determination of rate coefficients, since a direct experimental determination of rate coefficients is often laborious, time-consuming, and even problematic, leading to errors up to $\pm$ 30%.

Parametrized Trajectory Method

Considering the energetic environment inside CI-MS drift tube, rates obtained at thermal conditions cannot be applicable as such in practical applications. Under the PTR/CI-MS highly energetic conditions, the rate coefficients can be obtained by parameterized trajectory calculations as given by Su appropriate at center-of-mass kinetic energy and higher effective temperature. The parametrized rates are expressed by the following equations

$$ \frac{\rm k_{capture-com}}{\rm k_{Langevin}} = K_{capture}(\tau, \epsilon),,
$$
where
\begin{equation}
\tau = \frac{\mu_{\rm D}}{\sqrt{\alpha T}},,
\end{equation}
and

$$\epsilon = \frac{\mu_{\rm D}}{\sqrt{\alpha KE_{\rm com}}},.$$

Su and co-workers simulated over 100 systems, processing 6000 trajectories.
The following parametric equation was derived proposed to fit the obtained simulation data:

begin{align}nonumber
K_{\rm capture}(\tau, \epsilon) =& 1+c_1\tau^{0.4}\epsilon^{2}S+c_2 (1-S)\label{paraKE}
& times\sin[c_3{c_4+ln(\tau)}]\tau^{0.6}\sqrt{(\epsilon-0.5)}
,,
end{align}
where
$c_{1} = 0.727143$, $c_{2} = 3.71823$, $c_{3} = 0.586920$ and; $c_{4} = 4.97894$.
%
The quantity
begin{align}
S = begin{cases}
exp[-2(epsilon-1.5)] & text{for } epsilon>1.5\
1 & text{for } epsilonle1.5
end{cases}
,.
end{align}

From above equations, the effective ion temperature could exceed 1000~K if the $E/N$ ratio is raised above 100~Td (where 1~$text{Td} = text{Townsend} = 10^{-21}~text{V},text{m}^2$).
Su provided an improved parameterization useful to compute the temperature- and KE-dependence on the reaction rates:

begin{equation}
label{k_cap}
rm k_{rm capture-com}=k_{rm Langevin} , it K_{capture}(tau,epsilon)
,.
end{equation}

In this formula,
$K_{rm capture}(tau,epsilon)$ is the ion-molecule capture-rate coefficient at a given center-of-mass KE.

$K_{rm capture}$ is a function
of two reduced parameters:

begin{eqnarray}label{tau}
tau&=&frac{mu_{rm D}}{sqrt{alpha T}}
,,
\label{epsilon}
epsilon&=&frac{mu_{rm D}}{sqrt{alpha, KE_{com}}}
,.
end{eqnarray}

The parametrized quantity $K_{rm capture}(tau,epsilon)$, incorporating the dipole locking effect, is the result of the calculation of several thousand trajectories. When addressing experiments carried out at well-controlled temperature and KE conditions, we expect PTR rates to lie in between $rm k_{rm ADO}$ and ${rm k}_{rm capture}(T,{rm CT})$ $rm k_{rm cap}(T,{rm CT})$ estimates, most likely closer to ${rm k}_{rm capture}(T,{rm CT})$. The rate coefficients, ${rm k}_{rm capture-com}$, ${rm k}_{rm capture-com}$ at $(T_{rm eff})$ with center-of-mass kinetic energy, provide useful indications for PTR-MS measurements where thermal and kinetic energy conditions of the reactants are not so well under control.

Overall, the collision models discussed above have their own pro and cons applicable to experimental conditions. The parametrized trajectroty method is considered best fit under highely energetic experimental conditions of PTR-MS instrument and frequently used for the calculations of rate coefficients.